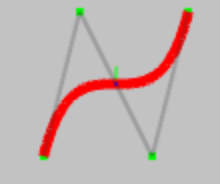
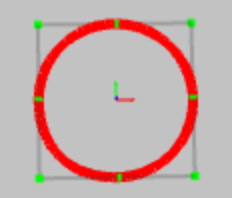
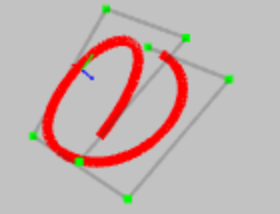
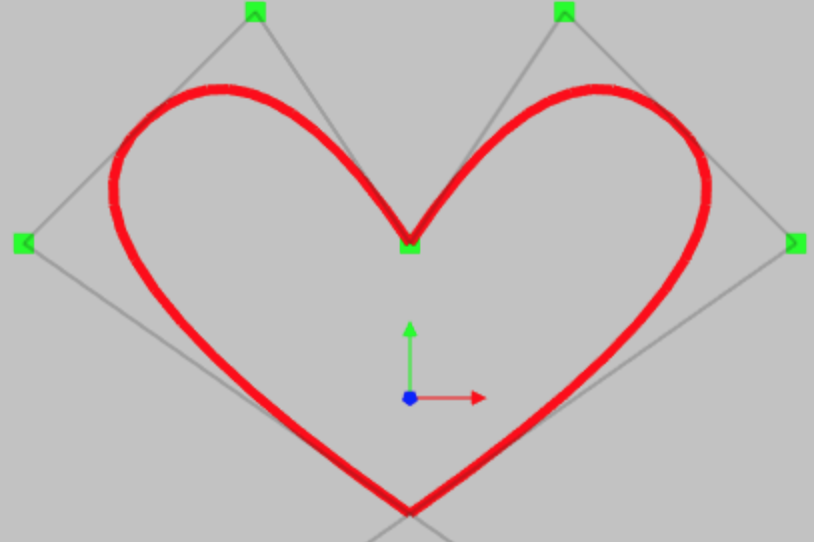
Non Uniform Rational B-Spline is a mathematical model to represent the free form curves and surfaces in computer
graphics. It is mostly used in Computer Aided Design (CAD) and creating characters for video games. The
mathematics behind NURBS is very vast and complex, but this nurbs-calculator covers only the evaluation part of
NURBS curves. And I have tried to make it as simple as possible, so that anyone can understand NURBS without
knowing the complex mathematics.
Evaluation means finding the coordinates of a point on the curve, corresponding to some parameter.
Curve parameters:
A NURBS curve can be created by just 3 parameters – degree, control point and knot vector. The term knot vector
is very confusing. Actually it’s just a sequence of some real numbers, in non-decreasing order.
Degree and order:
It is the measure of curvature of the curve. A curve with degree 1 is called as linear curve, with degree 2
is called as quadratic and degree 3 is called as cubic. In most of NURBS applications you will find curves
of degree 2 and 3, only. The degree of the curve is integer and should be > 0. Order of the curve =
degree + 1.
Control points:
The control points determine the shape of the curve. Each point is having 4 float values – x position, y
position, z position and weight of the control point. The minimum number of control points required to
render a NURBS curve is the same as the order of the curve. So you need atleast 4 control points for degree
3 curve.
U parameter:
In mathematics, the equation of a curve can be expressed as a function of an independent variable, called
as a parameter. In nurbs-calculator I call this parameter as u parameter. U parameter is used to calculate
the coordinates of a point, on the curve, from its parametric equation. Generally it is assumed that u is 0
at the start of the curve and 1 at the end. So at middle of the curve the value of u will be 0.5. Let's
assume that there is a line starting at (1,1) and ending at (2,2). Also assume that u=0 at start and u=1 at
end. If you are asked to find the coordinates of point, which lies at middle of the line, then in
mathematical term you will say that what should be coordinates of point at u=0.5. You can provide this u
value to the parametric equation of line and calculate the coordinates at middle point.You can also assume
that u=1 at start and u=2 at end or u=10 at start and u=100 at end. It is your assumptions which defines the
middle point of the curve, so for 0< u < 1, middle point is at u = 0.5, for 1 < u < 2, middle is
at u = 1.5 and for 10 < u < 100 middle is at u=55.
Knot vector:
As mentioned earlier, knot vector is a sequence of some real numbers, in non-decreasing order. This
sequence depends on the assumption of u values. If you are assuming that u varies from 0 to 1, then knot
vector is sequence of numbers, between 0 and 1. So basically knot values are u values. There is no
significance of each knot value separately. It is the sequence, which is important. The total number of
knots = number of control points + degree + 1. If degree of the curve is 2 and there are 4 control points,
then there will be total 7 knot values. A curve will be called as Non-Uniform, if the sequence of these knot
values is non-uniform (e.g 0.0, 0.4, 0.5, 0.6, 0.9, 0.95, 1.0 ) and called as uniform if this sequence is
uniform (e.g. 0.0, 0.167, 0.333, 0.5, 0667, 0.833, 1.0).
Knot multiplicity:
Multiplicity means repetition of knot values. Multiplicity is a property of knots that refers to the number
of control points associated to a knot. On a cubic curve (degree 3), a knot can have a multiplicity of 1, 2,
or 3, but not more than 3. Similarily for degree 2 curve the multiplicity can’t be more than 2. If knot
values have multiplicity = degree + 1 at the start, then curve will be clamped at start, that means the
curve touches the first control point. If the multiplicity < (degree+ 1) at start, then the curve will
not touch the first control point and the curve will start at u = k[p], where p=degree. Same is applicable
for the end knots.If the multiplicity at the end is < (degree + 1), then the curve will not touch the
last control point and curve will end at u=k[m-p], where m = (total number of knots - 1). That means, if
knot vector is = {0, 0.111, 0.222, 0.333, 0.445, 0.556, 0.667, 0.778, 0.889, 1.0} for degree 2 curve, then
the curve will start from u = 0.2, which is k[2] and end at u=0.778, which is k[7]. If the multiplicity >
(degree + 1), then the curve will split in disjoint parts and the control point will be unused.
These terminolgies have been explained in simple way and may not represent the exact definition. To
understand these terms in details, please visit CS3621 Introduction to Computing with Geometry
Course Notes or read The NURBS Book. NURBS
and its properties are also explained on Rhinoceros - NURBS and
NURB curves - a guide for the
uninitiated .
WebGL (Web Graphics Library) is a JavaScript API for rendering interactive 3D computer graphics and 2D graphics
within any compatible web browser (reference - wiki - webGL). In
nurbs-calculator I have used three.js to render the nurbs curves, so that a curve
can be viewed in 3D. Three.js is a cross-browser JavaScript library/API used to create and display animated 3D
computer graphics in a web browser (reference - wiki -
three.js). Three.js uses WebGL.